Profession : casser les codes
Alice Pellet-Mary, chargée de recherche CNRS en informatique.

Portrait d’Alice Pellet-Mary
« J’ai un parcours très classique ». C’est avec cette phrase qu’Alice Pellet-Mary décrit son cursus. Il n’en est rien. Brillant, il l’est assurément. Après le baccalauréat, Alice enchaîne avec succès une classe préparatoire en mathématiques et physique puis le concours d’entrée à l’ENS de Lyon en parcours mathématiques-informatique. Après un master de recherche en informatique, elle obtient l’agrégation de mathématiques. « Dès le lycée, j’ai eu envie de faire de la recherche » et Alice se donne les moyens de ses ambitions. Après une thèse au Laboratoire d’informatique du parallélisme (LIP) [1] et une année de post-doctorat à la KU Leuven, Alice posera ses valises à Bordeaux. Elle intégrera en février 2021 l’Institut de Mathématiques de Bordeaux (IMB) [2] en tant que chargée de recherche CNRS. Elle sera également membre de l’équipe-projet Inria « LFANT » (Inria, CNRS, université de Bordeaux) et y poursuivra ses travaux de thèse.
Rien de classique donc chez Alice qui s’est imposée comme une brillante chercheuse et a cultivé les échanges entre mathématiques et informatique.
« La limite entre mathématiques et informatique est floue »
Difficile parfois de différencier les mathématiques et l’informatique dans les travaux de recherche et particulièrement dans le domaine d’Alice Pellet-Mary : la cryptographie, la science des codes secrets.
Ou plutôt la cryptanalyse : « La cryptanalyse, c’est casser les codes secrets ». Un domaine qu’elle découvre très tôt et qui la fascine dès le lycée : « Je voulais faire de la cryptographie depuis la terminale ». Alice n’est pas la seule à avoir été fascinée par le décodage des messages secrets. On chiffre des messages depuis au moins 8 000 ans. Le principe est de trouver une transformation de symboles d’un langage (les lettres ou les mots par exemple) qui soit difficilement inversible. L’original doit être difficile à retrouver sans indication.
Les besoins de chiffrement sont aujourd’hui beaucoup plus importants. La sécurité des cartes bancaires, le commerce électronique, le wifi, les téléphones portables… Toutes ces technologies reposent sur la mise en œuvre concrète de méthodes de cryptographie. L’un des principaux objectifs est de garantir la confidentialité des messages. Une fois codé, on utilise le plus souvent une clé pour retrouver le message caché. Cette clé peut se présenter sous plusieurs formes : mots ou phrases, procédure pour préparer une machine de chiffrement, données informatiques codées …
Fin programmée pour le protocole RSA
Le protocole RSA est un algorithme de cryptographie reposant sur un principe relativement simple : l’utilisation de deux clés. Une clé publique chiffre et une clé privée déchiffre des données confidentielles. Sans cette clé privée, impossible de décoder les messages. « Grâce à ça, n’importe qui peut m’envoyer des messages. Par contre, si les personnes ne trouvent pas ma clé privée, ils ne peuvent pas retrouver mes messages. »
Le protocole RSA est aujourd’hui l’un des plus utilisés pour chiffrer des données. On estime que plus de 300 millions de programmes installés peuvent l’utiliser, pour sécuriser les transactions de commerce électronique. Tout pourrait être bouleversé par l’arrivée sur le marché des ordinateurs quantiques. Au lieu d’utiliser les règles de la physique classique, cette nouvelle classe d’ordinateurs s’appuie sur les propriétés de la physique quantique, la discipline qui décrit le monde à l’échelle des particules plus petites qu’un atome. Pour ces objets extrêmement petits, les lois obtenues après de nombreuses expériences sont très différentes de celles dont nous avons l’habitude à notre échelle de tous les jours. Un fonctionnement totalement différent pour les ordinateurs et qui pourrait mettre à mal tous nos protocoles de chiffrement.
« Certains problèmes sont grandement accélérés par les ordinateurs quantiques : c’est le cas du décryptage du protocole RSA ».
Alice Pellet-Mary, novembre 2020
Pour le moment, les ordinateurs quantiques ne sont qu’à l’état de prototype. Mais Il faut déjà penser à l’après-quantique ! « C’est le problème avec la cryptographie : un protocole est jugé sûr tant qu’on ne sait pas le casser. Mais quand il est cassé, c’est trop tard ». Il faut donc anticiper la fin de l’utilisation du protocole RSA et se tourner vers d’autres systèmes de cryptographie, utiles pour protéger nos données. Et les chercheur·es s’intéressent déjà à trouver des alternatives crédibles. C’est le sujet des travaux d’Alice, en particulier, l’étude des réseaux euclidiens.
Cacher un message dans une grille
La cryptographie à base de réseaux euclidiens est une alternative qui s’est clairement démarquée durant cette dernière décennie de recherche. Un réseau euclidien, c’est une grille de points régulièrement espacés. Les angles ne sont pas forcément droits et la grille, pas forcément de dimension 2. « En informatique, on aime bien les puissances de deux. Donc je travaille plutôt en dimension 512 ou 1024. » Il est possible de chiffrer des données à partir de cette grille : il suffit de sélectionner des points du réseau au hasard pour former un message.
Dans cette grille en dimension 2, il est possible d’atteindre tous les points gris en se déplaçant uniquement le long des lignes en pointillés. Ces lignes sont formées à partir des flèches bleues u et v, qu’on appelle des vecteurs. Ces u et v sont des segments de droite orientés et qui permettent de décrire la grille de manière exacte.
Il est également possible d’atteindre tous les points gris en se déplaçant le long des lignes verticales et horizontales en trait plein grises, formées à partir des vecteurs x et y rouges, plus petits.
Comment retrouver les x et y à partir de u et v ? C’est tout le travail d’Alice Pellet-Mary.
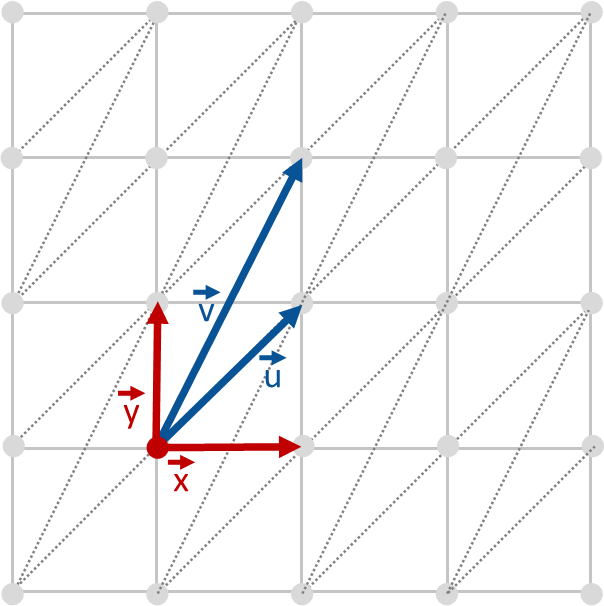
Grille de dimension 2 et vecteurs permettant de la parcourir entièrement
Pour casser facilement les codes produits à partir des réseaux euclidiens, il faut résoudre un problème fondamental : le problème du plus court vecteur. En connaissant déjà des vecteurs longs permettant de se déplacer dans la grille, comment retrouver des vecteurs plus petits pour faire exactement la même chose ? « C’est un problème beaucoup plus récent : essayer de trouver des algorithmes qui permettent d’atteindre ces vecteurs courts dans des réseaux. »
Hackeuse ? Non ! Chercheuse !
La cryptographie à base de réseaux euclidiens fait donc intervenir des calculs relativement simples, mais semble très complexe à casser et devrait être résistante au passage à l’ordinateur quantique. S’ils ne sont pas encore utilisés, les réseaux euclidiens intéressent l’American National Standards Institute. D’ici quelques années, les systèmes de chiffrement aux États-Unis pourraient donc s’appuyer sur les travaux d’Alice.
Au quotidien, Alice teste la résistance des techniques de cryptographie à base de réseaux euclidiens en améliorant petit à petit les algorithmes permettant d’obtenir des vecteurs courts. Mais elle est loin d’être une hackeuse : « L’avantage de la recherche, c’est que nous, on est censé avoir des intentions nobles. Quand on a cassé un protocole, on le dit publiquement. On dit aux gens de ne plus l’utiliser. On ne va pas détourner de l’argent. » Ce qui rend un protocole sûr, c’est justement le fait que les chercheur·es aux intentions louables aient essayé de le casser sans succès. Et Alice est confiante quant à la résistance de protocoles de chiffrement par les réseaux euclidiens. « Honnêtement, je ne pense pas qu’on arrivera à casser les réseaux. Mais nos recherches aboutissent tout de même ». Les algorithmes s’améliorent, mais le temps pour craquer les réseaux euclidiens reste encore beaucoup trop long.
Être une chercheuse en informatique
L’informatique et les mathématiques sont encore des domaines de recherche où les femmes sont peu nombreuses. En 2015, dans le domaine des mathématiques et conception de logiciel, 14 % des chercheur·es en entreprise sont des femmes. Trois ans après l’obtention d’un doctorat, les conditions d’emploi des femmes sont systématiquement moins favorables que celles des hommes : moins de postes et moins de postes stables. Elles ne représentent que 23 % des enseignant·es-chercheur·es titulaires dans ces disciplines. [3]

Carottes et carrés de chocolat forment un réseau euclidien de
dimension 2
La question du genre ne s’est pourtant jamais posée pour Alice et être une femme n’a jamais été un obstacle : « J’avais une idée et je me suis simplement laissée porter par cette idée ». Durant son doctorat, elle obtient la prestigieuse bourse française L’Oréal-UNESCO Pour les Femmes et la Science. Une reconnaissance de son travail mais aussi 15 000 € qui lui ont permis de partir deux mois aux États-Unis afin de participer à un rassemblement en Californie de chercheur·es spécialistes en cryptologie. « C’était la première fois que j’écrivais un dossier pour recevoir de l’argent, j’avais l’impression d’avoir passé une étape supplémentaire en tant que chercheuse ». Et Alice Pellet-Mary a passé une nouvelle étape : obtenir un poste fixe afin de poursuivre ses recherches.
Bordeaux pour étendre son réseau
Alice n’a pas choisi l’IMB par hasard : « L’avantage d’être à Bordeaux, c’est de pouvoir travailler avec des spécialistes de théorie des nombres. » Ses travaux de recherche s’orientent de plus en plus vers ce domaine précis des mathématiques et Alice a des idées plein la tête : « J’aimerais bien voir si certains travaux réalisés sur les codes correcteurs peuvent être appliqués aux réseaux ».
Un code correcteur permet de vérifier s’il y a une erreur dans les données. Par exemple, les deux derniers chiffres de votre numéro de sécurité sociale servent à vérifier qu’il n’y a pas d’erreur dans les nombres précédents. Ce code correcteur peut être plus poussé et corriger des erreurs. C’est le cas pour les communications wifi, jamais parfaites. Le code correcteur agit pour ne pas avoir besoin de renvoyer le message en intégralité.
Les codes correcteurs sont déjà utilisés en cryptographie depuis au moins les années 80. Mais depuis quelques années, des améliorations techniques liées à l’algèbre et la théorie des nombres ont permis d’améliorer l’efficacité de ces codes. Et c’est une bonne nouvelle pour Alice ! Les protocoles de cryptographie à base de code correcteur sont en effet très proches des protocoles à base de réseaux euclidiens. « Il y a toujours eu pas mal d’échanges entre les deux communautés, avec des gens qui utilisent des techniques de code pour améliorer les réseaux et vice versa. » Une opportunité pour Alice qui veut voir si ces améliorations peuvent être utiles à ses travaux. « Mon espoir c’est exactement ça : essayer de transférer des techniques des codes aux réseaux. » Une piste prometteuse qui lui permettrait peut-être de casser les codes !
Aurore VALEX
« Je n’aurais pas été là…
… s’il n’y avait pas eu d’exercice de cryptographie en mathématiques en terminale. »
C’est en terminale S qu’Alice Pellet-Mary découvre le principe de la cryptographie. Pour un devoir maison de mathématiques, elle doit retrouver un code secret. Et c’est la révélation. Alors en classe préparatoire, lorsqu’elle doit chercher un sujet de Travail d’initiative personnelle encadré ou TIPE (un travail dans le but de faire découvrir aux étudiant·es la démarche scientifique), elle s’oriente naturellement vers la cryptographie. « Il y a des moments où il faut choisir et pour moi, ça n’a jamais été difficile. Je savais que j’aimais la cryptographie, j’ai continué à suivre la voie facile ! » Une voie « facile », qu’elle continue de suivre aujourd’hui.
[1] Laboratoire d’informatique du parallélisme (LIP) (ENS de Lyon, Université Claude Bernard Lyon 1, CNRS, Inria).
[2] Institut de Mathématiques de Bordeaux (IMB) (CNRS, Université de Bordeaux, Bordeaux INP).
[3] Vers l’égalité femmes-hommes ? Les chiffres clés. 2019. Enseignement supérieur, recherche et innovation. DGESIP/DGRI/SIES. Sous-direction des systèmes d’information et des études statistiques. Disponible à l’adresse : https://cache.media.enseignementsup-recherche.gouv.fr/file/Brochures/32/8/parite2018_stats_A5_11d_908328.pdf
